Pytorch는 BackPropagtion을 구현할 때 Autograd 방식으로 쉽게 구현할 수 있도록 되어 있다.
BATCH_SIZE = 64
INPUT_SIZE = 1000
HIDDEN_SIZE = 100
OUTPUT_SIZE = 10BATCH 크기 64가 의미하는 것은 한 번에 들어가는 데이터의 양이다. INPUT의 크기는 학습 시킬 데이터의 양이다. OUTPUT은 말그대로 출력 데이터의 크기이다.
x = torch.randn(BATCH_SIZE,
INPUT_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = False)
y = torch.randn(BATCH_SIZE,
OUTPUT_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = False)
w1 = torch.randn(INPUT_SIZE,
HIDDEN_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = True)
w2 = torch.randn(HIDDEN_SIZE,
OUTPUT_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = True)
x :
torch.randn는 (0,1) 정규분포에서 샘플링한 값이다. INPUT 크기 1000개의 벡터를 BATCH의 크기 64개 만든다.
dim = (64,1000) requires_grad는 Gradient를 의미한다.
y :
Output과의 오차를 계산하기 위해 Output 크기를 10으로 설정
w1:
Input과의 크기가 동일하고 행렬 곱을 통해 100개의 데이터 생성 (1000,100) requires_grad = True, Gradient 계산(backpropagation을 통해 w1 업데이트)
w2:
w1과 x를 행렬 곱한 결과에 계산할 수있는 차원이어야한다. w1과 x의 곱은 (1,100) 이다 이것을 (100,10) 행렬을 통해 Output을 계산할 수 있도록 w2 모양 설정. requires_grad = True, Gradient 계산(backpropagation을 통해 w2 업데이트)
learning_rate = 1e-6
for t in range(1,501):
y_pred = x.mm(w1).clamp(min=0).mm(w2)
loss = (y_pred-y).pow(2).sum()
if t % 100 == 0:
print('Iteration: ',t,'\t',"Loss: ",loss.item())
loss.backward()
with torch.no_grad():
w1 -= learning_rate * w1.grad
w2 -= learning_rate * w2.grad
w1.grad.zero_()
w2.grad.zero_()
learning_rate : 학습률 Gradient 계산 결괏값에 learning_rate를 곱해서 업데이트 한다.
mm(matmul) : Input 값인 x를 w1과 matrix multiple x X w1
clamp : 비선형함수 적용
$y_i$ = \begin{cases} \text{min} & \text{if } x_i < \text{min} \\ x_i & \text{if } \text{min} \leq x_i \leq \text{max} \\ \text{max} & \text{if } x_i > \text{max} \end{cases}
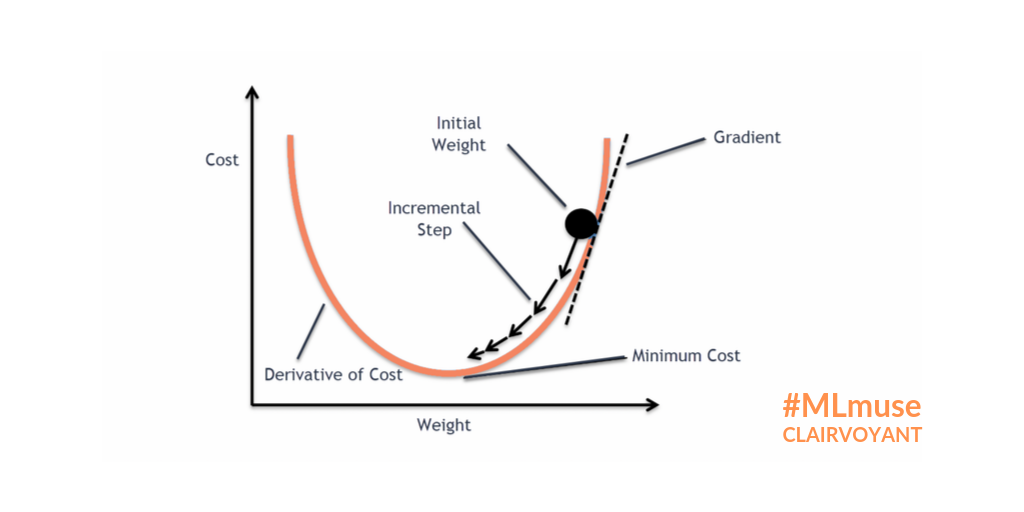
w1.grad.zero_ : Gradient 값을 초기화해 다음 반복문에 진행할 수 있도록 Gradient 값을 0으로 설정한다.
Iteration: 100 Loss: 673.0462646484375
Iteration: 200 Loss: 8.727155685424805
Iteration: 300 Loss: 0.18558651208877563
Iteration: 400 Loss: 0.004666611552238464
Iteration: 500 Loss: 0.00030295629403553903중요한 것은 gradient 값이 초기화되도 backward 메소드를 통해 backpropagation을 진행할 때 gradient 값을 새로 계산한다.
'🐍 Python' 카테고리의 다른 글
| [Code-Server] 코드 서버에서 주피터 노트북 사용하기 (0) | 2021.07.11 |
|---|---|
| [Code-Server] import-im6.q16: unable to open X server 에러 (0) | 2021.07.11 |
| [Jupyter Notebook] 주피터 노트북 셀 스크립트 너비 조절(cell script option), 판다스 너비 조절 (0) | 2021.03.21 |
| [Data Crawling] Spongebob - 1 (0) | 2021.03.16 |
| Matplotlib 한글 폰트 적용 (0) | 2021.02.13 |
Pytorch는 BackPropagtion을 구현할 때 Autograd 방식으로 쉽게 구현할 수 있도록 되어 있다.
BATCH_SIZE = 64
INPUT_SIZE = 1000
HIDDEN_SIZE = 100
OUTPUT_SIZE = 10BATCH 크기 64가 의미하는 것은 한 번에 들어가는 데이터의 양이다. INPUT의 크기는 학습 시킬 데이터의 양이다. OUTPUT은 말그대로 출력 데이터의 크기이다.
x = torch.randn(BATCH_SIZE,
INPUT_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = False)
y = torch.randn(BATCH_SIZE,
OUTPUT_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = False)
w1 = torch.randn(INPUT_SIZE,
HIDDEN_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = True)
w2 = torch.randn(HIDDEN_SIZE,
OUTPUT_SIZE,
device = DEVICE,
dtype = torch.float,
requires_grad = True)
x :
torch.randn는 (0,1) 정규분포에서 샘플링한 값이다. INPUT 크기 1000개의 벡터를 BATCH의 크기 64개 만든다.
dim = (64,1000) requires_grad는 Gradient를 의미한다.
y :
Output과의 오차를 계산하기 위해 Output 크기를 10으로 설정
w1:
Input과의 크기가 동일하고 행렬 곱을 통해 100개의 데이터 생성 (1000,100) requires_grad = True, Gradient 계산(backpropagation을 통해 w1 업데이트)
w2:
w1과 x를 행렬 곱한 결과에 계산할 수있는 차원이어야한다. w1과 x의 곱은 (1,100) 이다 이것을 (100,10) 행렬을 통해 Output을 계산할 수 있도록 w2 모양 설정. requires_grad = True, Gradient 계산(backpropagation을 통해 w2 업데이트)
learning_rate = 1e-6
for t in range(1,501):
y_pred = x.mm(w1).clamp(min=0).mm(w2)
loss = (y_pred-y).pow(2).sum()
if t % 100 == 0:
print('Iteration: ',t,'\t',"Loss: ",loss.item())
loss.backward()
with torch.no_grad():
w1 -= learning_rate * w1.grad
w2 -= learning_rate * w2.grad
w1.grad.zero_()
w2.grad.zero_()
learning_rate : 학습률 Gradient 계산 결괏값에 learning_rate를 곱해서 업데이트 한다.
mm(matmul) : Input 값인 x를 w1과 matrix multiple x X w1
clamp : 비선형함수 적용
$y_i$ = \begin{cases} \text{min} & \text{if } x_i < \text{min} \\ x_i & \text{if } \text{min} \leq x_i \leq \text{max} \\ \text{max} & \text{if } x_i > \text{max} \end{cases}

w1.grad.zero_ : Gradient 값을 초기화해 다음 반복문에 진행할 수 있도록 Gradient 값을 0으로 설정한다.
Iteration: 100 Loss: 673.0462646484375
Iteration: 200 Loss: 8.727155685424805
Iteration: 300 Loss: 0.18558651208877563
Iteration: 400 Loss: 0.004666611552238464
Iteration: 500 Loss: 0.00030295629403553903중요한 것은 gradient 값이 초기화되도 backward 메소드를 통해 backpropagation을 진행할 때 gradient 값을 새로 계산한다.
'🐍 Python' 카테고리의 다른 글
| [Code-Server] 코드 서버에서 주피터 노트북 사용하기 (0) | 2021.07.11 |
|---|---|
| [Code-Server] import-im6.q16: unable to open X server 에러 (0) | 2021.07.11 |
| [Jupyter Notebook] 주피터 노트북 셀 스크립트 너비 조절(cell script option), 판다스 너비 조절 (0) | 2021.03.21 |
| [Data Crawling] Spongebob - 1 (0) | 2021.03.16 |
| Matplotlib 한글 폰트 적용 (0) | 2021.02.13 |
